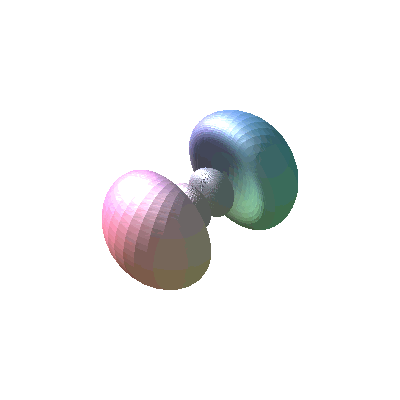We consider here the relationship between 3333 First we start with only the angular parts. For these are the spherical harmonics  

These are complex. Note that the dependence is the same; it depends only on l and the absolute value of m. We can plot the squares of the magnitudes as a function of and and colour them according to the phase. Red means a phase of zero (positive real number) and cyan means a phase of (negative real number). The phase runs in opposite directions for these two spherical harmonics. The z axis is pointing up and towards the viewer, the x axis is pointing forward and to the left and the y axis is back and to the right. 

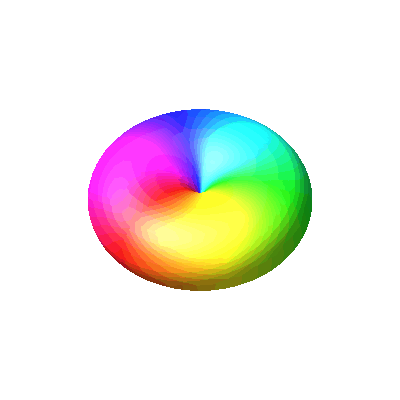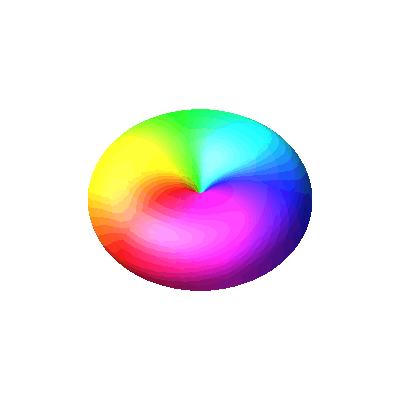Y1,1 or p1	Y1,-1 or p-1

If we take linear combinations of these we get the more usual real p_x and p_y angular functions: 

and 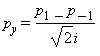.  We can plot them in the same way, plotting their squares as a function of and . Again red means a phase of zero (positive real number) and cyan means a phase of (negative real number). 

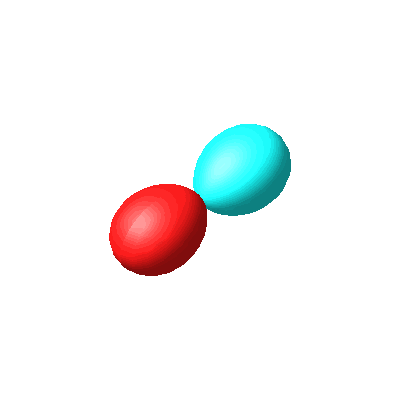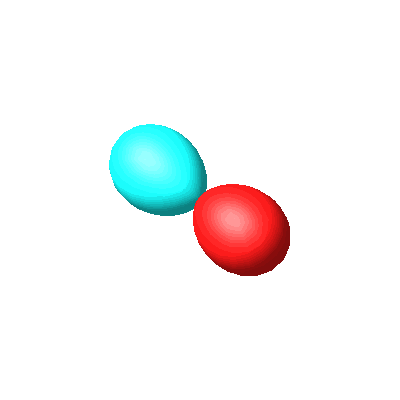px	py

These functions have angular nodes at certain values. cos() is zero for in the opposite directions of  90 and 270 degrees, giving a single vertical nodal plane that includes the y and z axes. Likewise sin() is zero at 0 and 180 degrees giving a vertical nodal plane that includes the x and z axes. Notice that if we were working with, say, m=3 and m=-3, the phase would show three repeated colour sequences in a full turn, we would get cos(3) and sin(3), and there would be three vertical nodal planes. 

So far we have only plotted angular functions, but now we focus on the 3 hydrogen orbital, which is the product of the angular function above and a radial function, which is given in atomic units as 

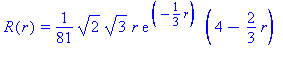
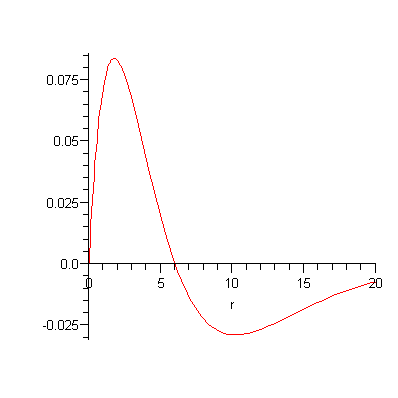
(To convert to SI units, divide every r by a₀ and multiply the expression by .) So there is a radial node at r = 6. If we put both the radial and angular parts together we get the complete function  

The subscripts of the orbitals (x, x²-y² etc.) are found by converting the spherical coordinates back to cartesian coordinate. Here we see that rsin()cos() is x, so we can write it as 

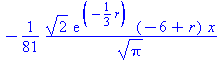
Note that we get rid of all the angles but we are allowed to leave rs in the expression. We can make a contour plot of a section of the wavefunction through the x-y plane. The radial node is the blue circle. The y axis is an angular node (plane in 3-D). 

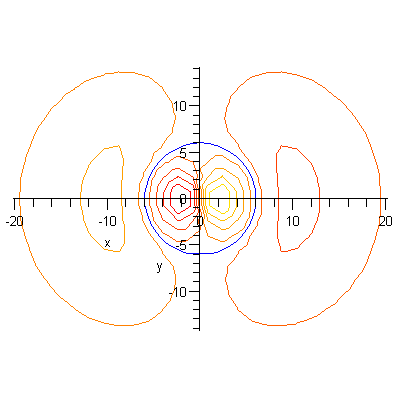
The usual plot is a 3-D plot of a contour of the wavefunction enclosing a certain probability. The 90% contour for the 3p_x orbital is at a wavefunction value of 0.00303 in atomic units (it is non-trivial to calculate this number). 

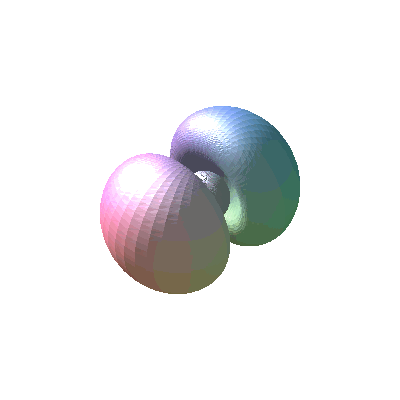
We can see the inner lobes a bit more clearly if we look at a contour that encloses less probability.