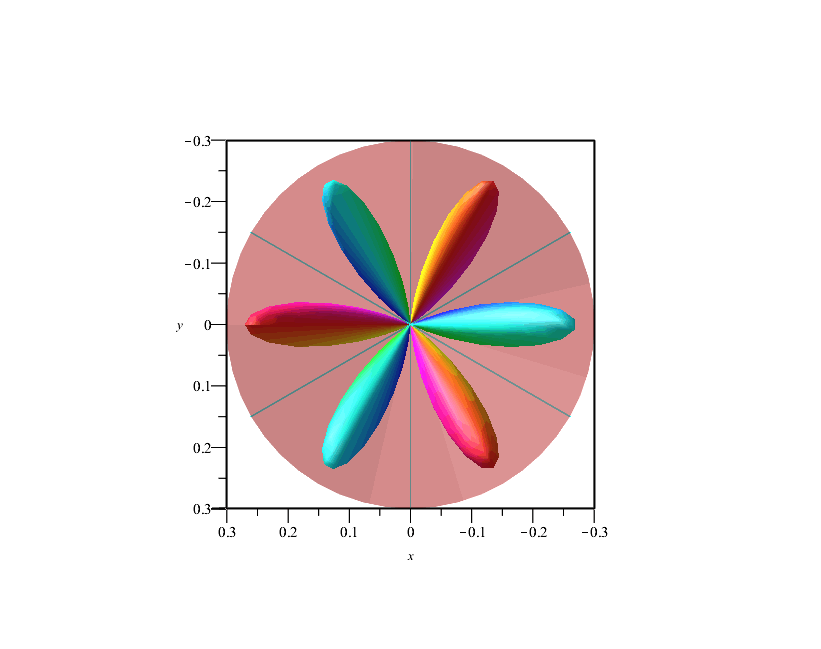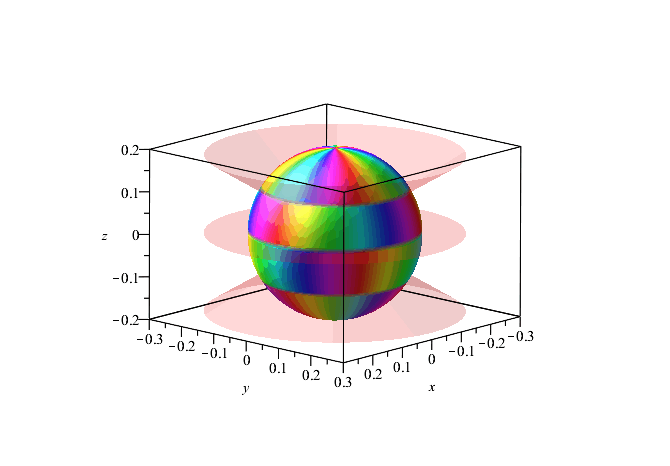
Plot of l = 6, m = 3 spherical harmonic plotted as phase colours (red = 0, cyan = π) on the surface of a sphere.  There are m = 3 rainbows of colour going around the z axis. The l - |m| = 6 - 3 = 3 cone (θ) nodes may be seen in pink.  

Magnitude squared of l = 6, m = 3 spherical harmonic plotted as a function of θ and ϕ and coloured according to phase. The three rainbows are perhaps easier to see, and the cones are now separating different pieces of the orbital. 

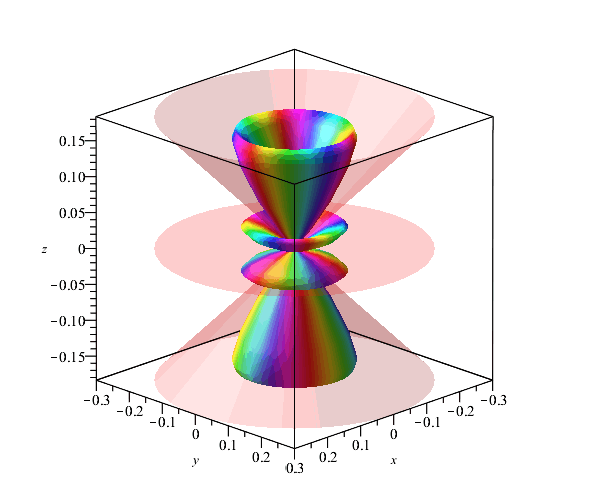
Magnitude squared of the real combination plotted as a function of θ and ϕ and coloured according to phase. We have the same function of θ and therefore the same cone nodes, but instead of 3 rainbows we now have three vertical nodal planes (ϕ nodes). First picture has only the cones showing: 

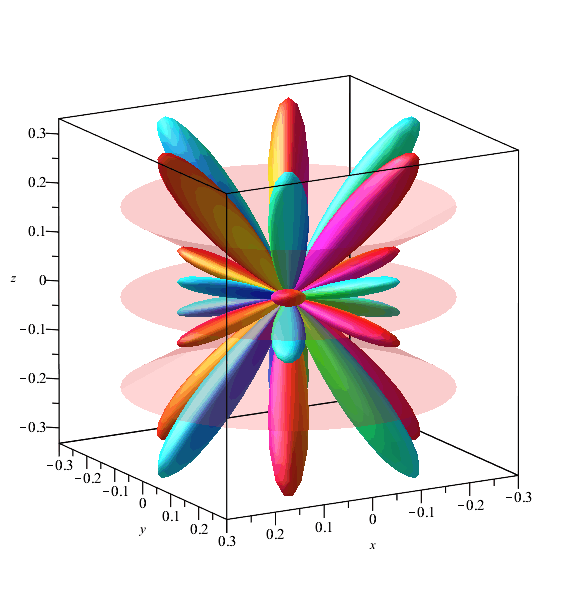
Next we add the vertical plane nodes: 

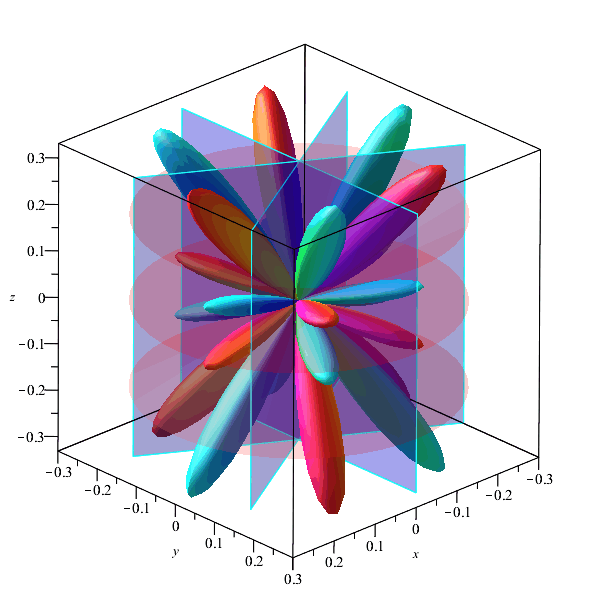
If we look down on this, we see that the xz plane is not a node. This means that this must be the cos(3ϕ) function, which results from adding the two spherical harmonics.