Evaporation Studies Using Stable Isotopes

Ongoing research has emphasized development and refinement of theoretical models describing isotopic behaviour at the air-water interface, including practical applications such as tracing of the evaporation process. A brief theoretical review is presented below.

Theoretical Background

The stable isotopes of oxygen () and hydrogen () are nearly ideal tracers of water cycling processes as they are mass-conservative, and occur naturally within the water molecule (i.e. , , and ). Systematic isotopic labelling of water parcels within the hydrologic cycle (i.e. atmospheric moisture, precipitation, surface water, groundwater etc.) has been recognized globally, and is known to occur due to isotopic fractionations which accompany phase transitions and diffusive transport, owing mainly to slight differences in molecular behaviour of the rare, heavy isotopic species. Such passive labelling has been applied for example, to study mixing between compartments in the hydrologic cycle during snowmelt and runoff events. For open-water bodies, the isotopic fractionation occurring during evaporation is most important, as it imparts a distinct enrichment of heavy isotopes in lake water with respect to inflow sources and precipitation.

For an evaporating water body, isotopic fractionation occurs at the air-water interface due to slightly lower vapour pressures and retarded rates of molecular diffusion of the two rare, heavy isotopic species of water and with respect to the common, light isotopic species . These fractionation processes, which typically give rise to evaporating moisture which is isotopically depleted (lighter) with respect to the residual liquid, have been exploited to study evaporation by several approaches, including: (1) tracing of isotopically-depleted evaporate admixtures to the atmosphere as recorded in the deuterium excess of precipitation; (2) tracing of vapour fluxes to the atmosphere and partitioning by measuring isotopic gradients above the evaporating surface; and, (3) tracing isotopic buildup which occurs in the residual liquid, i.e. in lakes. Lake studies must apply an isotope mass balance approach to account for exchange between lake water, inflow and precipitation, and as a consequence have been a powerful tool for study of water balance processes rather than evaporation alone. An algebraic description of the fractionation process during evaporation, and isotope mass balance is given below. A similar description of isotopic fractionation accompanying freezing and thawing is also presented and provides a basis for discussing the significance of these processes in cold-regions lakes. A representative cross-section of the broad spectrum of water balance studies using isotopic methods is given elsewhere in this volume.

Isotopic ratios are reported in standard "" notation as deviations in per mil (‰) from the Vienna-SMOW (Standard Mean Ocean Water), such that _SAMPLE = 1000((R_SAMPLE/R_SMOW)-1), where R is ¹⁸O/¹⁶O or ²H/¹H. ¹⁸O and ²H values cited herein are normalized to -55.5‰ and -428‰, respectively, for SLAP (Standard Light Antarctic Precipitation) (see Coplen, 1996). Analytical uncertainties are ±0.1 ‰ for d¹⁸O and ±2 ‰ for d²H.

Isotopic fractionation at the air-water interface

Isotopic fractionation during evaporation can be described as a combination of fractionations occuring by exchange between water molecules in liquid and vapour (in thermodynamic equilibrium), and diffusion of water molecules from the liquid to vapour phase (also called kinetic or transport fractionation). In the case of a water body in thermodynamic equilibrium with the atmosphere i.e. when there is no humidity gradient, the equilibrium fractionation factor (⁺) between liquid and vapour can be represented as

(1)

where and are the ratios of heavy isotopic species to the common isotopic species in liquid and vapour, respectively where , and ⁺ > 1 such that the rare, heavy isotopic species is more abundant in the liquid phase. Isotopic differences between coexisting phases are by convention discussed in terms of isotopic separation factors. In this case, the equilibrium isotopic separation between liquid and vapour () is given by

(2)

and and are the -notation equivalents of and , respectively.

Numerous laboratory measurements of have been conducted for oxygen and hydrogen over wide range of temperatures such that their values are reasonably constrained for use in water balance studies (Fig. 1). Notably, values are substantially better defined than the analogous kinetic isotopic separations (discussed later). For example, one standard deviation for the results at 10°C is about 0.24 and 2.1 for oxygen and hydrogen, respectively, which is similar in magnitude to the analytical uncertainty.

Figure 1. Variation in equilibrium isotopic separation between liquid and vapour for oxygen () and hydrogen () as a function of temperature (°C). Based on the data of: 1- Majoube (1971); 2-Bottinga and Craig (1969); 3-Jakli and Stachewski (1977), and; 4-Kakiuchi and Matsuo (1979).

The most commonly used values for oxygen and hydrogen, valid for the temperatures of 0 to 100°C, are respectively (Majoube 1971):

(3)

(4)

which corresponds to an isotopic enrichment in and , respectively, of about 9.79 ‰ and 85 ‰ at 0°C and 11.71 ‰ and 112.3 ‰ at 20°C, respectively. The ratio varies over this temperature range between 8.68 to 9.59 and is similar to the slope of the Meteoric Water Line (Craig 1961) in versus space.

For the case of evaporation into undersaturated air, the isotopic separation between liquid and vapour typically exceeds due to kinetic effects. The total isotopic separation () in this case is

(5)

where is the kinetic isotopic separation which is dependant on the evaporation mechanism. Craig and Gordon (1965) first proposed the use of a Langmuir-type linear resistance model to describe transport of the isotopic species through the boundary layer during constant evaporation i.e. constant vertical flux with no convergence or divergence in the air column. As summarized recently in Gat (1996) the model depicts transport of vapour through a series of sublayers, including in order: a saturated sub-layer above the air/water interface, where relative humidity and the isotopic ratio in the saturated sub-layer according to Eq. (1) is ; a boundary layer consisting of a diffusive sublayer and turbulently mixed sublayer in which transport occurs by diffusion and turbulent transfer, respectively, and finally; the free-atmosphere where , and being the specific humidity in the saturated sublayer and the free atmosphere, respectively.

Evaporation (through the boundary layer) of water and the rare, heavy isotopic species (either or ) can be written, respectively as (Gat 1996):

(6)

(7)

where is the isotopic ratio in the free-atmosphere; is the resistance to transport of water through the boundary layer, and being the diffusive and turburbulent contributions to respectively; and is the analogous resistance to transport of the rare, isotopic species. Note that as turbulent transfer does not cause further isotopic fractionation and the resistance to transport of the rare, heavy isotopic species is dependent solely on the diffusive resistance.

The isotopic composition of the evaporating moisture flux (or evaporate), equal to the ratio of evaporation of the rare isotopic species and water can then be determined by

(8)

expressed in notation where yields

(9)

where , , and are the isotopic compositions of the evaporate, the liquid (assumed to be well-mixed), and the free atmosphere, respectively.

For the case of resistance to mixing in the liquid phase, Craig and Gordon (1965) propose

(10)

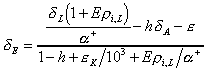
where is the resistance to mixing of the rare, heavy isotopic species in the liquid phase. The effect of any resistance, although widely presumed to be negligible, will cause the evaporate to be slightly enriched relative to the liquid as an enriched boundary layer will form in the near-surface liquid. It is important to note that Eqs. (9) and (10) represent the net evaporation process accounting for both evaporation and molecular exchange (condensation) from the water surface to the free air.

According to the Craig and Gordon model, the kinetic isotopic separation is defined as

(11)

The kinetic fractionation constant has been shown to be related to the ratio of the resistance to transport of water and the rare isotopic species through the boundary layer such that

(12)

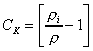
and

(13)

where and are the molecular diffusivities in air of water and the the rare, heavy isotopic species, respectively determined experimentally by Merlivat (1978) and others, and is a turbulence parameter. Experimental evidence suggests that the turbulence parameter varies depending on the evaporation mechanism such that for mean turbulent flow, for laminar flow and for static transport (Gat 1996). This is consistent with a transient eddy model of a randomly renewed surface layer as proposed by Brutsaert (1965, 1975). As noted in an earlier review (Gonfiantini 1986), , which corresponds to values of 14.3 ‰ and 12.5 ‰ for oxygen and hydrogen, respectively, appears to reasonably represent open-water evaporation conditions (on the time-scale of water balance investigations) that are most frequently observed. In contrast, is more appropriate for describing evaporation from soils where static transport dominates.

The parameter , was recently introduced by Gat (1995) to account for situations where the evaporation flux has a significant influence on the free-air, as for the atmosphere on the leeward side of large water bodies such as the Great Lakes of North America (Gat et al.). In this situation precipitation The adjusted humidity , in this case, is the humidity of the atmosphere following the admixture of evaporate. In principle, also can be used to describe any situation where humidity and sampling of vapour for isotopic analysis is conducted within the turbulently mixed sublayer.

A summary of the available estimates of the kinetic fractionation constants is given in Fig. 2 based on experimentally determined D/Di values for static transport (Merlivat 1978) at n=1, for mean turbulent (n=1/2) and laminar flow (n=2/3) based on the model of Brutsaert (1965), and for transitional regimes assuming continuity. Roughness reynolds numbers are also shown for comparison.

Fig. 2 Roughness reynolds number zo+=u*zo/v where zo is surface roughness length, u* is friction velocity, v is viscosity of air.

Figure 3. Humidity dependence of the kinetic fractionation e_K for oxygen and hydrogen at the air-water interface and its effect on the total isotopic fractionation e , where e = e*+ e_K , and e* is the equilibrium fractionation and e_K is the kinetic fractionation (area between curves).

Isotope mass balance

For open-water periods when evaporation plays a role in the water balance surface waters become enriched in the heavy isotopic species. During such periods, the water-mass and isotope-mass balance for a well-mixed reservoir, assuming constant density of water, may be written respectively as

(14)
(15)

where V is the volume of the reservoir, t is time, dV is the change in volume over time interval dt, I is inflow, Q is outflow, E is evaporation, and , , and are the isotopic compositions of the reservoir, inflow, outflow, and evaporative flux, respectively. Providing that isotopic compositions of components in eq. (2) can be measured or estimated, and given that systematic isotopic enrichment occurs during exposure to evaporation under normal climate conditions, it is possible to combine eq. (1) and eq. (2) to solve for two unknown water balance components. While characterization of the isotopic composition of most components is possible through weighted sampling, is difficult to measure directly.

Constant Volume Models

Combining eqs. (2) and (3) and integrating between the limits and for time intervals where water balance fluxes and their isotopic compositions can be assumed constant and (i.e. hydrologic steady-state) yields

(18)

where is the initial isotopic composition of the reservoir, and is the steady-state isotopic composition the reservoir will attain as determined by.

(19)

where is the fraction of reservoir water lost by evaporation, as defined in previous studies and is the limiting isotopic composition under local climate conditions.

In the special case where reservoirs are large enough to buffer transient isotopic variations related to seasonality of hydroclimate conditions, and when long time intervals are considered, it can be assumed that the lake is also close to isotopic steady-state () and eq. (4) can be simplified to yield

(20)

which is a key relationship describing the dependency between the water balance of a large reservoir and its isotopic enrichment by evaporation . Atmospheric controls on this enrichment include and through their influence on and .

Figure 4. Schematic time-series of d¹⁸O enrichment in reservoirs for a range of x (evaporation/inflow). Humidity effects are also shown.