Ergodic Theory: An example

Ergodic theory is a branch of dynamical systems dealing with questions of averages. Many simple dynamical systems are known to be chaotic, which implies that long-term predictions are impossible from initial data with limited accuracy. Sometimes, ergodic theory can make predictions about the average behavior, even when systems are chaotic.

One of the simplest examples is given by iterating the map defined by T:[0,1]->[0,1], where T(x)=4x(1-x). This map is illustrated on the left. This map belongs to the family of Logistic maps which in turn is part of the more general family of unimodal maps. The Logistic maps are all of this form, except that the number 4 is replaced by a parameter a which is allowed to vary between 1 and 4. As a varies, the maps exhibit a large number of interesting 'bifurcations' and it has been relatively recently shown that a 'large set' of maps in the logistic family have an invariant density (see below).

The chaotic behaviour of the map is illustrated by the second figure which shows the orbits Tⁿ(x₁) and Tⁿ(x₂) for two points x₁ and x₂ which differ by 10^-8 and 1<=n<=40. Note that after about 24 steps, the orbits have diverged completely. This is typical behavior for chaotic systems and is sometimes referred to as sensitive dependence on initial conditions.

We see from this that long-term predictions are impossible in that given a point to finite precision, we cannot calculate accurately Tⁿ(x).

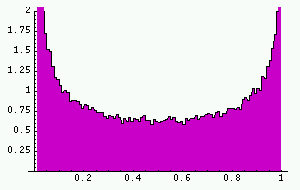In spite of this, it is possible to make good long-term average predictions. To produce this histogram, the interval was divided into 100 subintervals of length 0.01, and the proportion of time that the first 100000 points on the orbit of 0.3 spent in each subinterval was recorded. It is noticeable that this 'density' has a relatively smooth form. It turns out to be possible to calculate this density theoretically. It is called the 'invariant density' and the formula for it is p(x)=pi(x(1-x))^-1/2. This function is graphed below.

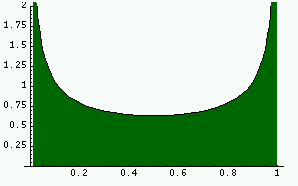It can be shown that for almost every initial point (in the sense of Lebesgue measure), the histogram produced by looking at the densities of orbits in [0,1] converges to the true invariant density as the number of points on the orbit tends to infinity and the number n of intervals in the histogram increases to infinity.

One important consequence of this is that if we want to calculate an average of a function along an orbit (an important example of this is in calculating Lyapunov exponents which measure `local stretching'), then we may instead calculate an average over the `phase space' ([0,1]). That is for a function f, we have that for almost all x, the average of f(Tⁱ(x)) as i runs from 1 to n converges to the integral of f(x)p(x) over [0,1], where p(x) is the invariant density function described above.

This is known as Birkhoff's Pointwise Ergodic theorem and this is one of the key results in ergodic theory. The theorem dates from 1927.

This is often described by saying that the time average and space average are equal.

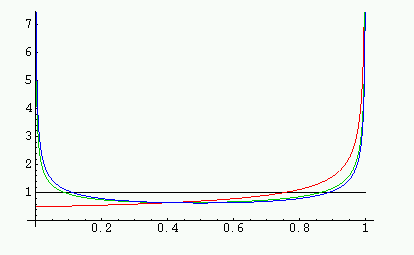Another way of finding the invariant density is to look for fixed points of the Ruelle-Perron-Frobenius operator. This is a linear map which allows one to look at the evolution of a family of densities. If one starts off with an initial distribution of measure on the interval, then applying the map stretches out the measure and `folds it over'. The new density at a given point x depends on the densities at the two preimages of x. Specifically, the new density is the sum of the densities at the preimages divided by the absolute value of the derivative of the map there. This map from the densities to themselves was introduced by Ruelle and is an important tool in ergodic theory. For the logistic map, if one starts off with an initial density f₀=1, and applies the operator to get a sequence f₁, f₂, f₃..., they converge rapidly to the true invariant density, p(x). In the figure f₀ is plotted in black, f₁ in red, f₂ in green and p(x) in blue.

Ergodic theory has advanced considerably since that time, but there are still a large number of accessible problems to work on and it continues to be an active field, with applications to many other areas of mathematics, including probability theory, information theory, differential geometry and number theory.