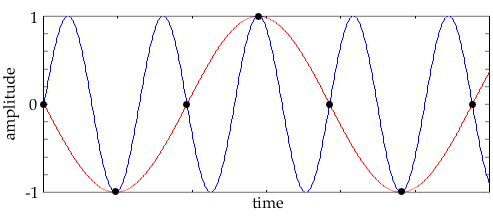

Example of undersampling, which causes aliasing. Let's say we want to sample the blue sinusoid, but we don't sample often enough. What happens is that the black dots, which are supposed to represent the higher frequency (blue) sinusoid, instead represent the lower frequency (red) sinusoid. The result is aliasing: you will hear the lower frequency, not the one you intended. This is known as aliasing or foldover.
NOTE: If you try to sample any frequency that is higher than half the sampling rate (called the Nyquist frequency), you will instead get:
SR - original frequency
EXAMPLE: If the sampling rate is 20,000 Hz, and the input frequency is 12,000 Hz (which is higher than the Nyquist freq of 10,000 Hz), the result will be 8,000 Hz, which is what you will hear.
Note that there is NO WAY to get around this mathematical fact!
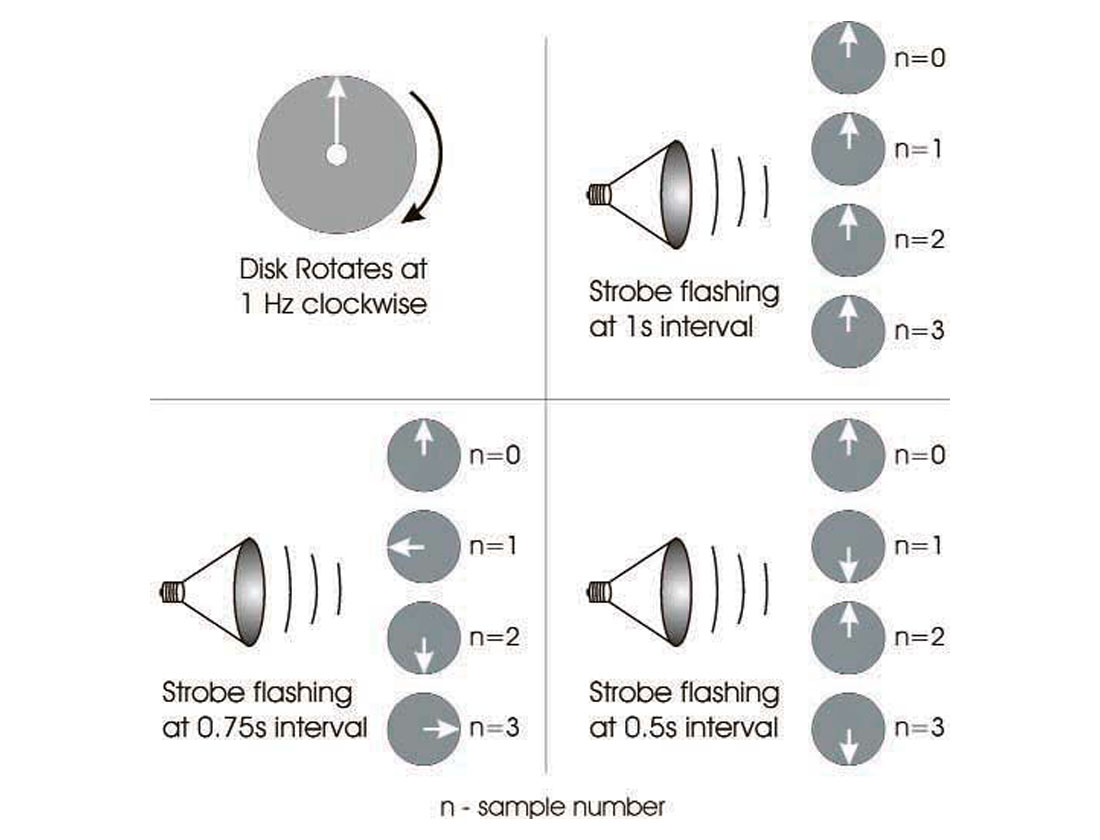
What causes the "wagonwheel effect" (a simple example of aliasing)?
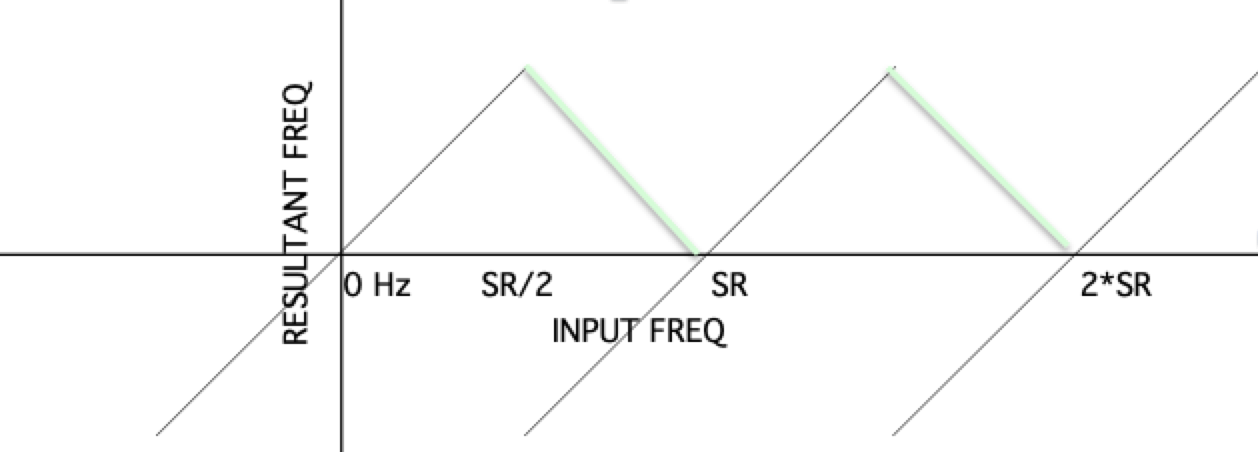
Here is a graph of aliasing that applies to the "wagon wheel" situation (on a TV screen), but it also applies to audio. Note that this goes on forever to the right (repeats forever). What is actually happening -- the frequency "jumps" from + to - at the SR/2 (Nyquist freq):
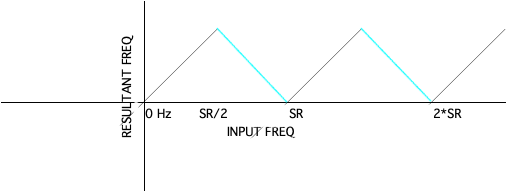
Note that we don't hear the jump to negative frequencies -- instead we just hear the "foldover" as the frequency ramps smoothly back down to 0.
What it sounds like is the green descending line (the absolute value, since we don't hear negative frequencies).