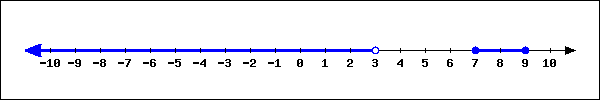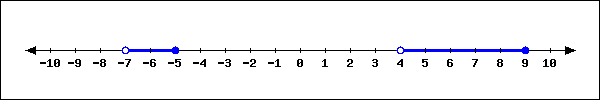Skip to main content

Precalculus Review Materials

Jane Butterfield, Gary MacGillivray

Section 1.6 Exercises

These are the exercises in Module 1.
Add the fractions, and reduce your answer.
\(\frac{{3}}{{2}}+\frac{{17}}{{2}}\)
The reduced answer is
Answer.
\(10\)
Simplify the following fraction.
\({{\frac{2}{3}}} + {{\frac{3}{4}}} \div {{\frac{5}{4}}} - {{\frac{2}{3}}}\)
\({}={}\)
Answer.
\({\frac{3}{5}}\)
Solution.
We must follow the order of operations when simplifying this expression. Begin by doing the division.
\(\displaystyle{\begin{aligned}[t] {{\frac{2}{3}}} + {{\frac{3}{4}}} \div {{\frac{5}{4}}} - {{\frac{2}{3}}}\amp ={{\frac{2}{3}}} + {{\frac{3}{4}}} \cdot {{\frac{4}{5}}} - {{\frac{2}{3}}}\\ \amp ={{\frac{2}{3}}}+{{\frac{3}{5}}}-{{\frac{2}{3}}}\\ \amp = \frac{10}{15} + \frac{9}{15} - \frac{10}{15} \\ \amp = \frac{3}{5} \end{aligned} }\)
Divide one fraction into the other: \(\displaystyle{ \frac{7}{6} \div \left(-\frac{5}{4}\right) }\)
If needed, use an improper fraction in your answer. Don’t use a mixed number.
Answer.
\(-{\frac{14}{15}}\)
Solution.
When we do division with fractions, as with
\(\displaystyle{\frac{7}{6} \div \left(-\frac{5}{4}\right) }\)
we first change division to multiplication, and at the same time, flip the second fraction. In this case, we have
\(\displaystyle{\frac{7}{6} \cdot \left(-\frac{4}{5}\right) }\)
Then we do fraction multiplication as usual. The full process is:
\(\displaystyle{\begin{aligned}[t] \frac{7}{6} \div \left(-\frac{5}{4}\right) \amp = \frac{7}{6} \cdot \left(-\frac{4}{5}\right) \amp \hbox{We can divide the first denominator and the second numerator by 2.}\\ \amp = \frac{7}{3 }\cdot\left(-\frac{2}{5}\right) \\ \amp = -\frac{14}{15} \end{aligned} }\)
Subtract one fraction from the other: \(\displaystyle{\frac{9}{16} - \frac{15}{16}}\)
When needed, use an improper fraction in your answer. Don’t use a mixed number.
Answer.
\(-{\frac{3}{8}}\)
Solution.
To subtract two fractions with the same denominator, we simply subtract the numerators and keep the denominator unchanged.
\(\displaystyle{\begin{aligned} \frac{9}{16} - \frac{15}{16} \amp = \frac{9 - 15}{16} \\ \amp = \frac{-6}{16} \amp \hbox{We can reduce this by dividing 2 into both the numerator and the denominator. }\\ \amp = -\frac{3}{8} \\ \end{aligned} }\)
Evaluate this expression:
\(\displaystyle{ \left({{\frac{7}{4}}}-{{\frac{9}{20}}}\right)-5\left({{\frac{9}{20}}}-{{\frac{7}{4}}}\right)= }\)
Answer.
\({\frac{39}{5}}\)
Solution.
You might need to go back to previous units to review how to add fractions.
\(\begin{aligned} \left({{\frac{7}{4}}}-{{\frac{9}{20}}}\right)-5\left({{\frac{9}{20}}}-{{\frac{7}{4}}}\right) \amp = {{\frac{13}{10}}} -5\left({{\frac{9}{20}}}-{{\frac{7}{4}}}\right) \\ \amp = {{\frac{13}{10}}} -5\left({-{\frac{13}{10}}}\right) \\ \amp = {{\frac{13}{10}}} -\left({-{\frac{13}{2}}}\right) \\ \amp = {{\frac{39}{5}}} \end{aligned}\)
Evaluate this expression:
\(\displaystyle{ 8-2 [ 3-(6+5\cdot4)]= }\)
Answer.
\(54\)
Solution.
The bracket [ ] and parentheses ( ) have the same purpose. We usually use [ ] when ( ) are already used in the problem, so we can tell which pair are which.
\(\displaystyle{\begin{aligned}[t] \amp \phantom{={}} 8-2 [ 3-(6+5\cdot4)] \\ \amp = 8-2 [ 3-(6+20)] \\ \amp = 8-2 [ 3-26 ] \\ \amp = 8-2 [ -23 ]\\ \amp = 8 + 46 \\ \amp = {54} \end{aligned} }\)
Evaluate this expression:
\(2^4[2^5-2^3(2^1+2^4)] =\)
Answer.
\(-1792\)
Solution.
\begin{equation*} \begin{aligned} \amp \phantom{\mathrel{{}={}}}2^4[2^5-2^3(2^1+2^4)] \\ \amp =2^4[2^5-2^3(2+16)] \\ \amp =2^4[2^5-2^3\cdot18] \\ \amp =2^4[2^5-144] \\ \amp =2^4\cdot[-112] \\ \amp ={-1792} \\ \end{aligned} \end{equation*}
Evaluate this expression:
\(\displaystyle{ 6[16-3(7+8)] = }\)
Answer.
\(-174\)
Solution.
\(\begin{aligned} 6[16-3(7+8)] \amp = 6[16-3\cdot15] \\ \amp = 6[16-45] \\ \amp = 6\cdot[-29] \\ \amp = {-174} \end{aligned}\)
Rewrite the following as a perfect square.
\(169 s^{16} = \big(\) \(\big)^{2}\)
Answer.
\(13s^{8}\)
The expression
\(\frac{(2y^{5})^4}{4y^5}\)
equals \(cy^e\) where the coefficient \(c\) is , the exponent \(e\) of \(y\) is .
Answer 1.
\(4\)
Answer 2.
\(15\)
Find \(x\) if
\begin{equation*} \frac{(2.8)^x (2.8)^{-3}}{(2.8)^{-6}}=(2.8)^{4} \end{equation*}
\(x =\)
Answer.
\(1\)
Rewrite the following using a single exponent, and simplify. If
\begin{equation*} \left(8^{9 x}\right)^{8 + 6 n} = 8^{m} \end{equation*}
then \(m =\)
Answer.
\(72x+54xn\)
Let \(S=(-3,\infty)\text{,}\) \(T=(-\infty,-1]\text{,}\) and \(W=[-7,-1)\)
For each intersection or union, choose the correct notation for the resulting interval.
1. \((S \cup T)\)
2. \((S \cup W )\)
3. \((T \cap W)\)
4. \((S \cap T)\)
  1. \(\displaystyle [-7, -1)\)
  2. \(\displaystyle (-3, -1]\)
  3. \(\displaystyle [-7, \infty)\)
  4. \(\displaystyle (-\infty, \infty)\)
Answer 1.
\(\text{D}\)
Answer 2.
\(\text{C}\)
Answer 3.
\(\text{A}\)
Answer 4.
\(\text{B}\)
This exercise is concerned with operations with inequality and interval notations.
Match the sets and the inequalities by placing the letter of the inequality next to each set listed below:
  1. \(x\) is no more than \(19\)
  2. \(x\) is nonnegative
  3. All \(x\) in the interval \([-8,19)\)
  4. All \(x\) in the interval \((-8,19)\)
  1. \(\displaystyle x\leq 19\)
  2. \(\displaystyle -8\lt x\lt 19\)
  3. \(\displaystyle -8\leq x\lt 19\)
  4. \(\displaystyle x\geq0\)
Sketch the following sets on a piece of paper and write them in interval notation. Enter the interval in the answer box. You may use "infinity" for \(\infty\) and "-infinity" for \(-\infty\text{.}\) For example, you may write (-infinity, 5] for the interval \((-\infty,5]\text{.}\)
\(18 \le x \le 21\)
\(22 \lt x \le 27\)
\(-3 \lt x \lt 1\)
\(-4 \le x \lt 1\)
Answer 1.
\(\left[18,21\right]\)
Answer 2.
\(\left(22,27\right]\)
Answer 3.
\(\left(-3,1\right)\)
Answer 4.
\(\left[-4,1\right)\)
Solve each compound inequality. Write your answer in interval notation or if no solutions exist write no solutions.
(a) \(x\geq4\) and \(x\geq8\text{:}\)
(b) \(x\leq13\) and \(x\leq4\text{:}\)
Answer 1.
\(\left[8,\infty \right)\)
Answer 2.
\(\left(-\infty ,4\right]\)
Write interval notation for the given graph:
Answer:
Answer.
\(\left(-\infty ,3\right)\cup \left[7,9\right]\)
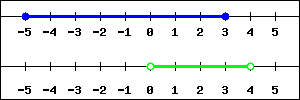
graph of two intervals.
For the graphs shown above, find the following:
  1. Write a compound inequality to describe the union of the points shown in the graphs.
Answer:
  1. Write a compound inequality to describe the intersection of the points shown in the graphs.
Answer:
Answer 1.
\(\left[-5,4\right)\)
Answer 2.
\(\left(0,3\right]\)
Express the inequality shown in the graph above using interval notation.
Answer:
Answer.
\(\left(-5,-2\right)\)
Write the interval notation for the given graph:
If the set includes more than one interval, they are joined using the union symbol U. We use the captial letter of “u” as the union symbol.
graph of an interval.
Answer:
Answer.
\(\left(-7,-5\right]\cup \left(4,9\right]\)
<Prev^TopNext>