Section 3.6 Exercises
These are the exercises in Module 3.
Note that many of these exercises contain images, which are by default not loaded. Make sure to click ’Make interactive’ on each in order to load the images.
Checkpoint 3.6.1.
Checkpoint 3.6.2.
Solve the following inequality. Enter the answer in interval notation.
\begin{equation*}
\frac{4 -x}{x-8} \ge 0
\end{equation*}
Answer:
Note: If the answer includes more than one interval, write the intervals separated by the “union” symbol, U. If needed, enter \(\infty\) as infinity and \(-\infty\) as -infinity.
Checkpoint 3.6.3.
Checkpoint 3.6.4.
Checkpoint 3.6.5.
The expression
\begin{equation*}
\frac{2^52^32^{-4}}{\sqrt{4^4}2^32^{-3}}
\end{equation*}
Checkpoint 3.6.6.
Checkpoint 3.6.7.
The expression
\((3 x^3 y^{\frac{-6}{7}})^5(4 y^2)^{\frac{1}{2}}\)
equals \(n x^r y^t\) where
\(n\text{,}\) the coefficient, is:
Checkpoint 3.6.8.
Checkpoint 3.6.9.
Checkpoint 3.6.10.
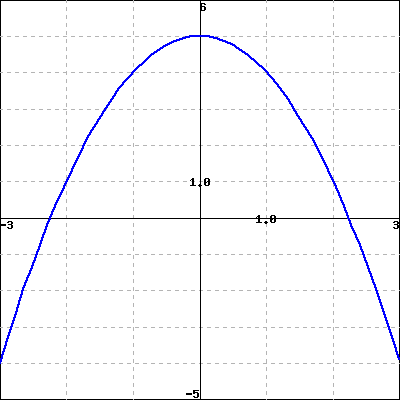
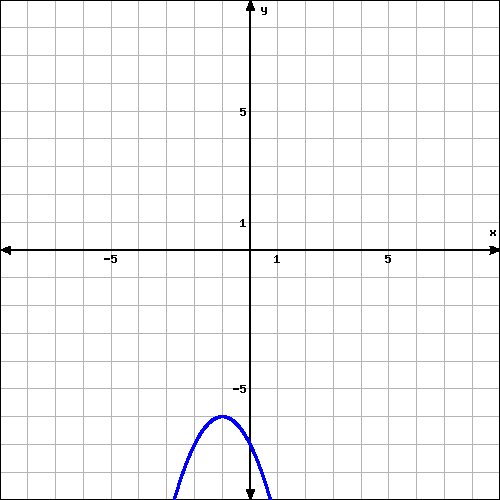
The equation of the graphed function is
-
\(\displaystyle y=-x^2 \)
-
\(\displaystyle y=x^2-5 \)
-
\(\displaystyle y=5-x^2 \)
-
\(\displaystyle y=5+x^2 \)
-
None of the above
Hint.
Look for evidence that will help eliminate wrong answers.
This graph has a maximum (highest \(y\) value), are there any answers you can eliminate because they don’t have maximums?
If more than one answer is left, can you eliminate any because you can see a point that is on the graph but does not satisfy the equation in that answer?
Solution.
A look at the graph gives us the following information.
-
The answer cannot be \(y=5+x^2\) since this graph has a maximum at \((0,5)\) and \(y=5+x^2\) has no maximum as \(x\) increases.
-
The answer cannot be \(y=x^2-5\) for two reasons.
-
The answer cannot be \(y=-x^2\) since when \(x=0, y=-x^2=0\) and we know from the graph that when \(x=0, y=5\)
To make sure we might want to check the remaining answer, \(y=5-x^2\text{.}\) It has the correct maximum at \((0,5\) and the graph looks like a parabola. If we were certain that the points at which the function corsses the \(x\)-axis were \((-\sqrt{5},0)\) and \((\sqrt{5},0)\) then we could be more sure, since just as the equation of a line can be found from knowing two points, the equation of a parabola can be found from knowing three points.
Checkpoint 3.6.11.
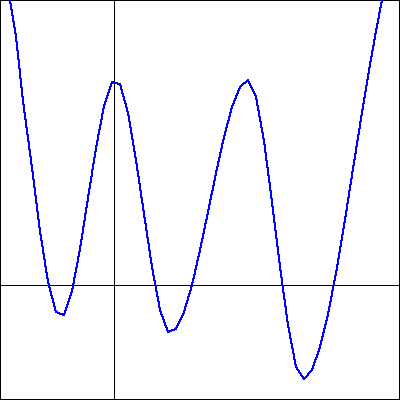
Use properties of the functions to match each of the following functions with its graph. Do not use your calculator.
1. \({-x^{2}+2}\)
2. \({\frac{-x\mathopen{}\left(3-x\right)^{2}}{3}}\)
3. \({\frac{x^{3}}{3}-\frac{x^{2}}{3}-3x+0.5}\)
4. \({\frac{-x^{3}}{3}+\frac{x^{2}}{3}+3x+0.5}\)
A
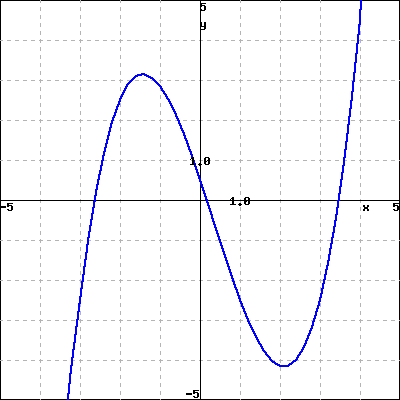
B
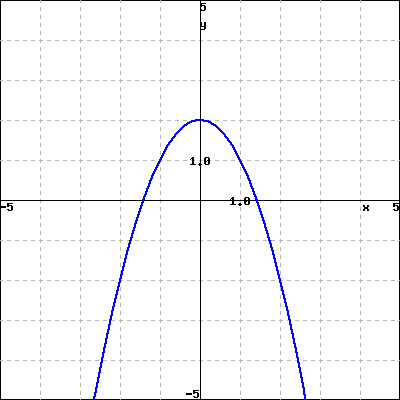
C
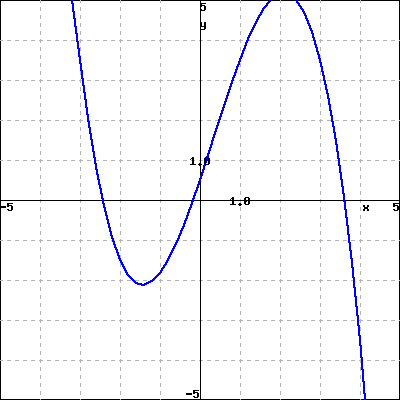
D
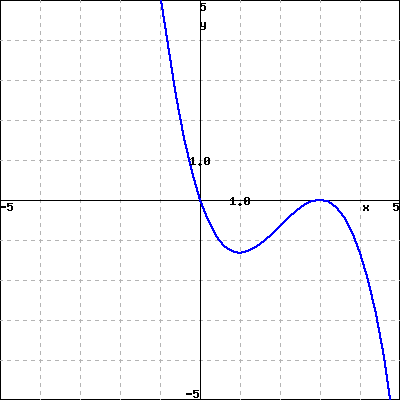
Checkpoint 3.6.12.
Checkpoint 3.6.13.
Tell whether the following ordered pairs are solutions to the given inequality.
\(y \le 4\)
-
\((-8,4)\)
-
\((0,0)\)
-
\((-5,-6)\)
-
\((0,8)\)
Solution.
We substitute \(y\) values from each ordered pair into the inequality \(y \le 4\) and see whether the inequality is true.
-
The ordered pair is \((-8,4)\text{.}\)\(\begin{aligned}[t] y \amp \stackrel{?}{\le} 4 \\ 4 \amp \stackrel{?}{\le} 4 \end{aligned}\)Since this inequality is true, \((-8,4)\) is a solution to the inequality.
-
The ordered pair is \((0,0)\text{.}\)\(\begin{aligned}[t] y \amp \stackrel{?}{\le} 4 \\ 0 \amp \stackrel{?}{\le} 4 \end{aligned}\)Since this inequality is true, \((0,0)\) is a solution to the inequality.
-
The ordered pair is \((-5,-6)\text{.}\)\(\begin{aligned}[t] y \amp \stackrel{?}{\le} 4 \\ -6 \amp \stackrel{?}{\le} 4 \end{aligned}\)Since this inequality is true, \((-5,-6)\) is a solution to the inequality.
-
The ordered pair is \((0,8)\text{.}\)\(\begin{aligned}[t] y \amp \stackrel{?}{\le} 4 \\ 8 \amp \stackrel{?}{\le} 4 \end{aligned}\)Since this inequality is not true, \((0,8)\) is not a solution to the inequality.
Checkpoint 3.6.14.
This exercise is not currently working as expected, and was removed August 2023.
Checkpoint 3.6.15.
Use properties of the functions to match each of the following functions with its graph. Do not use your calculator.
1. \(y +x \ge -3\)
2. \(x \le 2 \text{ and } y \ge 4\)
3. \(x+y \le 2\)
4. \(y \le -2\)
A
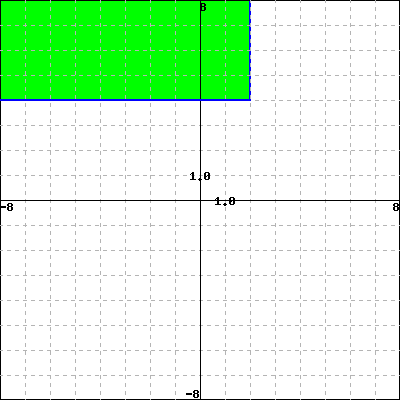
B
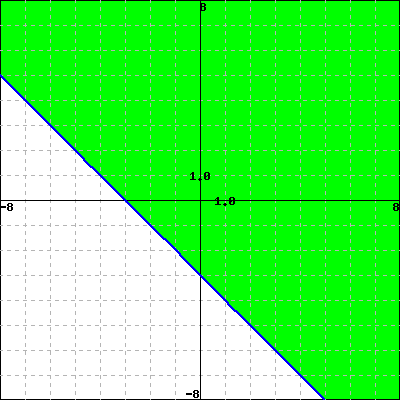
C
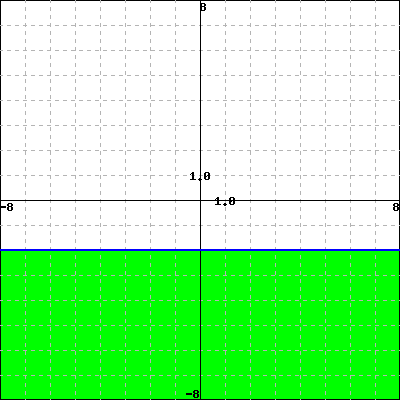
D
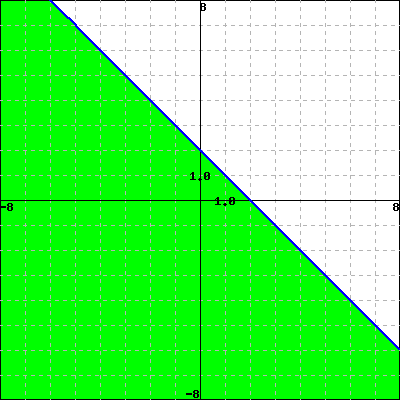
Checkpoint 3.6.16.
This exercise is not currently working as expected, and was removed August 2023.